Simple deepest regression method.

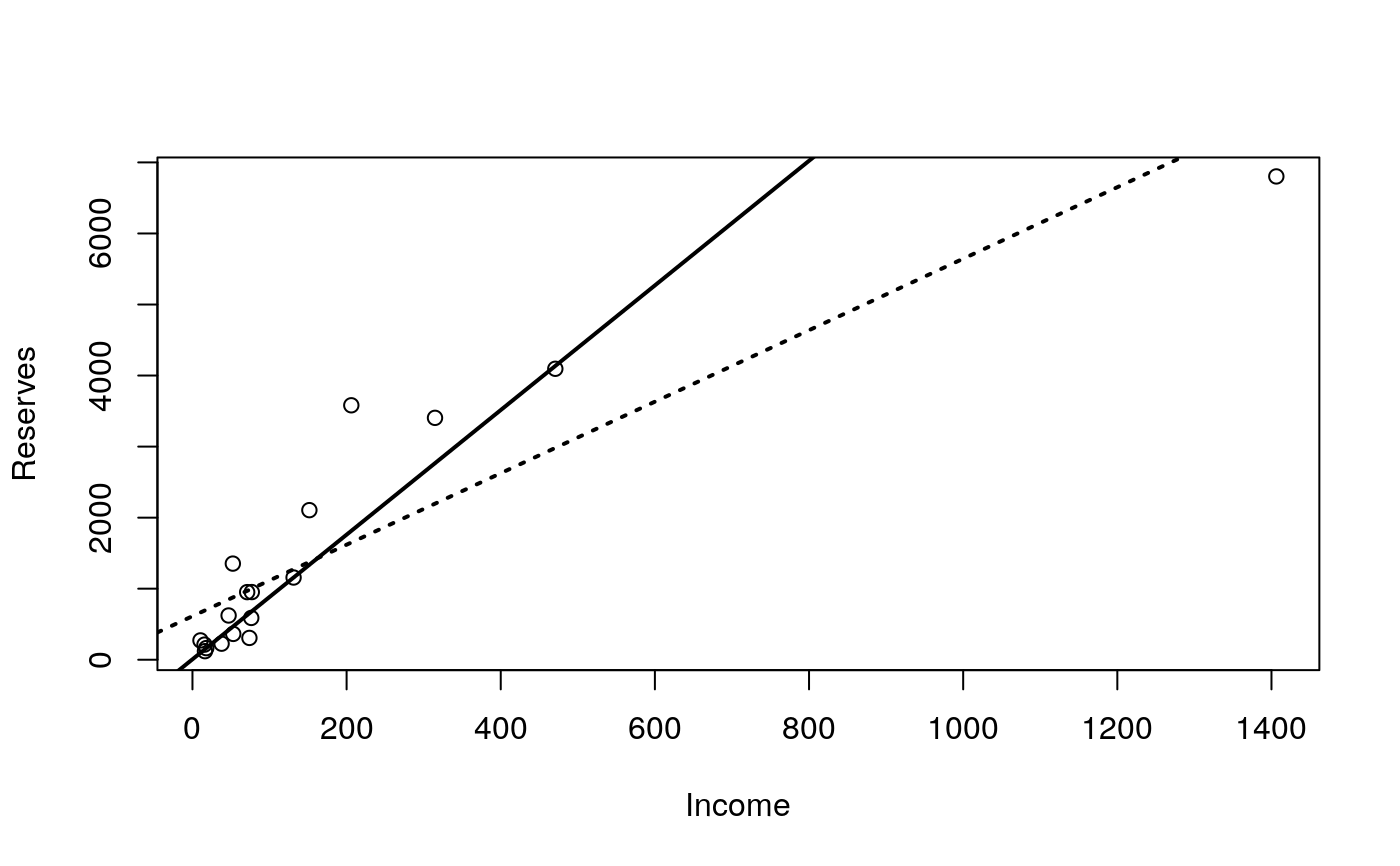
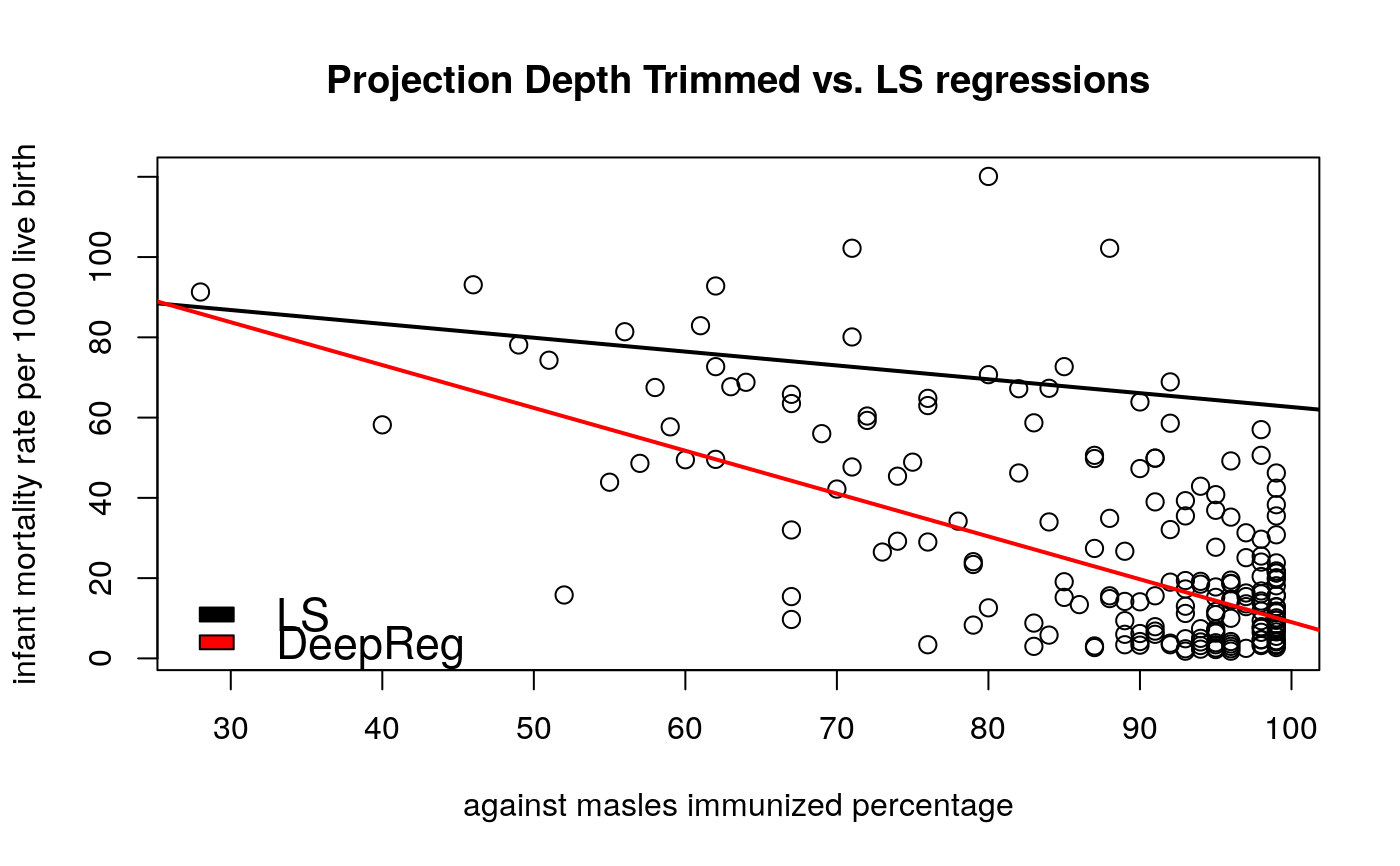
This function calculates deepest regression estimator for simple regression.

deepReg2d(x, y)

Arguments

x	Independent variable.
y	Dependent variable.

Details

Function originates from an original algorithm proposed by Rousseeuw and Hubert. Let \( {Z} ^ {n} = {(x_1, y_1), ..., (x_n, y_n)} \subset {{R} ^ {d}} \) denotes a sample considered from a following semiparametric model: \( {{y}_{l}} = {{a}_{0}} + {{a}_{1}}{{x}_{1l}} + ... + {{a}_{(d - 1)l}}{{x}_{(d - 1)l}} + {{\varepsilon }_{l}}, {l = 1, ..., n} \), we calculate a depth of a fit \( \alpha = (a_{0}, ..., a_{d - 1}) \) as \( RD(\alpha, {{Z} ^ {n}}) = {u \ne 0}\min\sharp {l: \frac{ {{r}_{l}}(\alpha) }{ {{u} ^ {T}}{{x}_{l}} } < 0, l = 1, ..., n} \), where \( r(\cdot) \) denotes the regression residual, \( \alpha = (a_{0}, ..., a_{d - 1}) \), \( {u} ^ {T}{x}_{l} \ne 0 \). The deepest regression estimator \( DR(\alpha, {{Z} ^ {n}}) \) is defined as \( DR(\alpha, {{Z} ^ {n}}) = {\alpha \ne 0}\,\arg\max\,RD(\alpha, {{Z} ^ {n}}) \)

References

Rousseeuw J.P., Hubert M. (1998), Regression Depth, Journal of The American Statistical Association, vol.94.

Examples

# EXAMPLE 1
data(pension)
plot(pension)
abline(
  lm(Reserves ~ Income, data = pension),
  lty = 3,
  lwd = 2) # lm
abline(
  deepReg2d(pension[, 1], pension[, 2]),
  lwd = 2) # deepreg2d

# EXAMPLE 2
data(under5.mort)
data(inf.mort)
data(maesles.imm)
data2011 <- na.omit(
    cbind(under5.mort[, 22], inf.mort[, 22],
    maesles.imm[, 22]))

x <- data2011[, 3]
y <- data2011[, 2]
plot(
  x, y,
  cex = 1.2,
  ylab = "infant mortality rate per 1000 live birth",
  xlab = "against masles immunized percentage",
  main = "Projection Depth Trimmed vs. LS regressions"
)
abline(lm(x ~ y), lwd = 2, col = "black") # lm
abline(
  deepReg2d (x, y),
  lwd = 2, col = "red"
) # trimmed reg

legend(
  "bottomleft",
  c("LS", "DeepReg"),
  fill = c("black", "red"),
  cex = 1.4,
  bty = "n"
)